|
The
purpose of filtering is always the same:
Make
the signal distinct and suppress the noise. We call it optimizing the signal/noise-ratio.
In general signal processing there is an extensive theory and a huge variety
of filters. For the Scorpion intensity profiles we have made a small, but
effective subset available. They can be chosen by 5 integer parameters. The
three first parameters decide a linear FIR filter consisting of a gaussian
smooth filter and differentiation. In praxis there will be a small set of
actual values of the possible ones. If we set the differentiation to zero,
we get a clean smooth filter suited to remove noise with small frequent
variations along the intensity profile. Below a set of such smooth filters
is graphically shown. (The numbers in parentheses are the smooth base and
smooth counter respectively.)
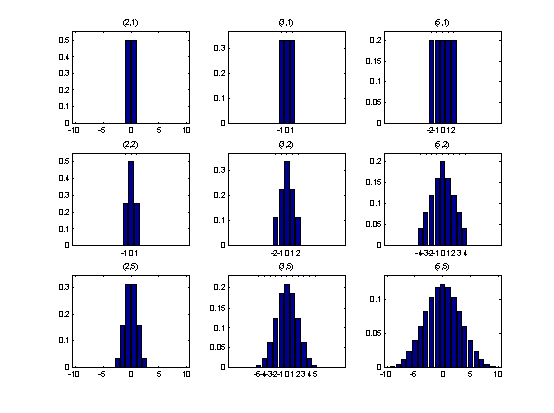
Generally
you can say that the wider and flatter the filter is, the more it smoothes.
The filter becomes wider both when the smooth base and smooth counter
increases. When the smooth counter increases the filter changes from
rectangular to more gaussian. When the smooth base increases, the width
increases more directly.
When
searching for intensity profile jumps, it is suitable to differentiate to
change the jumps into tops easy to detect. Differentiation however increases
the high frequent noise in the image. Thus it is wise to always combine
differentiation with smoothing. Below you see graphs of filters with first
order differentiation and varying degree of smoothing. As earlier we see
that the smooth base increases the width, while the smooth counter makes the
filter more gaussian.
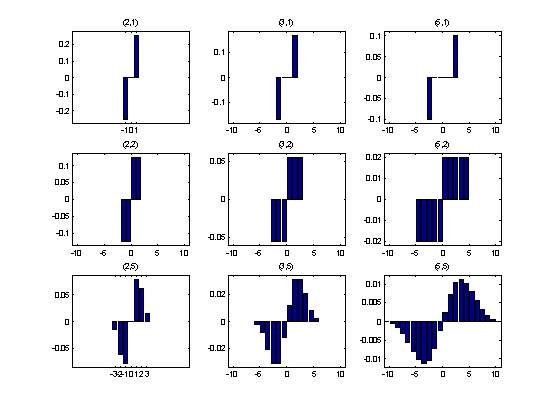
Higher order
differentiation is also possible, but rarely used since the noise is
increased. You may however compensate this by low pass filtering or
smoothing the curve. This results in wide filters and is only suited to
detect forms covering wider parts of the intensity profile. Second order
differentiation is however useful to detect narrow dark or light stripes in
the image. These will turn out as sharp tops and bottoms in the intensity
profile. But they can be difficult to detect because they may lay on varying
intensity levels and you get problems with finding a common threshold
setting to select the tops and bottoms you really want. If you use a second
order differentiation filter to see the sharp ripples in the intensity
profile, you will get tops that can be separated by a common threshold
setting. Below you see some examples of second order differentiation
filters:
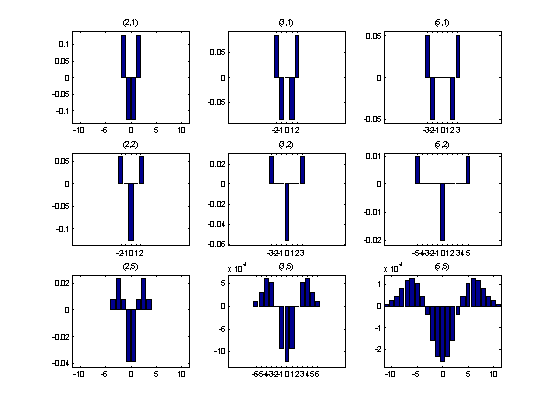
Observe
again the filter width increases with the smooth base, while the gaussian
form increases with the smooth counter.
|