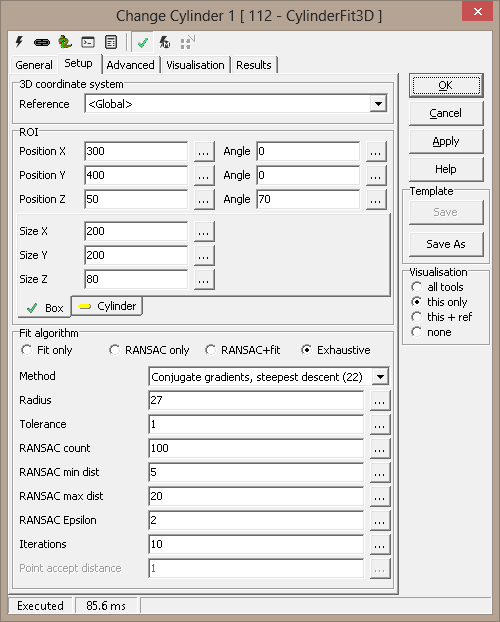
Setup3D
coordinate system
- Reference - select a 3D reference for position
and results
ROI
- See the term 3D ROI
(Note: Sphere ROI is not supported for this tool)
Note that the axis of a cylinder found must fall
within a cylinder described by the center of the ROI (x direction) and
the initial guess radius in its entire (x) extent. This means:
- If you have a cylinder ROI, a found cylinder will have
its axis close to the ROI axis, within the boundary set by the
initial guess radius (not the inner or outer ROI radii)
- With a box ROI, the ROI axis is defined as the center (in
y and z) of the box. This means you must make the ROI box wide
enough to enclose the axis of the cylinder you want to find.
Specifically, if your data set contains only points from one "side"
of the cylinder (as is common with GCPS), your ROI should include
the "other" (hidden) side of the cylinder as well.
Fit algorithm
- Fit only - run (possibly multipass - see Advanced) the
fit algorithm given by Method
- RANSAC only - run a single RANSAC fit only
- RANSAC + fit - run a single RANSAC fit, followed by (possibly
multipass - see Advanced) the fit algorithm given by Method
- Exhaustive - run RANSAC followed by a complete iterative fit
based on the algorithm given by Method
- Method -
- Random (10) - Naive implementation used primarily for testing
and debugging. It simply tests randomly in a region assumed to contain a
minimum. If the random point tested actually produces a smaller error,
the method jumps there and then continues. By slowly reducing the
randomness and size of the region, one increases the chance of stumbling
upon a global minimum. The method will converge, but not necessarily
fast.
- Conjugate gradients - This is a class of methods based on the
availability of derivatives of the error function, i.e., a gradient. In
its simplest con guration, this method performs the classic Steepest
Decent search for a minimum, which works by moving in the direction in
which the error decreases most rapidly, and moving an amount in this
direction which is foreseen to bring us to a point from which it is no
longer useful to continue in said direction. This is then repeated. For
many problems this can work just nicely, but the classic and simple
example for which this breaks down is the error function looking like a
long and slightly slanting valley . For this problem, Steepest Decent
will (from a high point) head straight towards the valley,
overshoot/undershoot slightly, and then in the next step also head
directly for the bottom of the valley , doing a much smaller step. The
sensible thing to do, take a long stride along the valley, will never be
a favoured move by this method, hence a very slow convergence. This
particular problem is eliminated by the conjugate gradient methods (of
which Steepest Decent is not a true case, rather a very reduced special
case). But still - these methods need the gradient, and a numerical
gradient will destroy some of the nice convergence properties of the
methods. There are three variations, documented in e.g. Numerical
Recipes:
- Fletcher-Reeves (20) - a proper conjugate gradient method
- Polak-Ribiere (21) - a proper conjugate gradient method
- Steepest descent (22) - see above
- Nelder Mead - This algorithm is not based on a gradient or
other derivative of the error function. In a sense, it can be compared
to the RandomMinimizer, except that it moves around in a much more smart
fashion than purely random. The method is based on having a simplex in
the search space for which the corners are evaluated. The simplex is
moved and transformed so as to continually shrink simultaneously with
the corner evaluations also decreasing, thus converging on what is hoped
to be a (global) minimum. How this transformation of the simplex is done
is not without freedom, there are some parameters to tweak, giving
variations of the method. With parameters as close to the original work
by Nelder and Mead as we have been able to figure out, we have made a
Classic Nelder-Mead , and with some more recent choices of parameters we
have found published on the internet, we made Variation I.
- Original (30) - see above
- Variation (31) - see above
- Radius - initial guess
- Tolerance - max deviation from initial guess
- Decimations - max number of iterations (for Exhaustive
search)
- RANSAC count - max RANSAC iterations
- Min dist - minimum distance between points considered for a
RANSAC search
- Max dist - maximum distance between points considered for a
RANSAC search
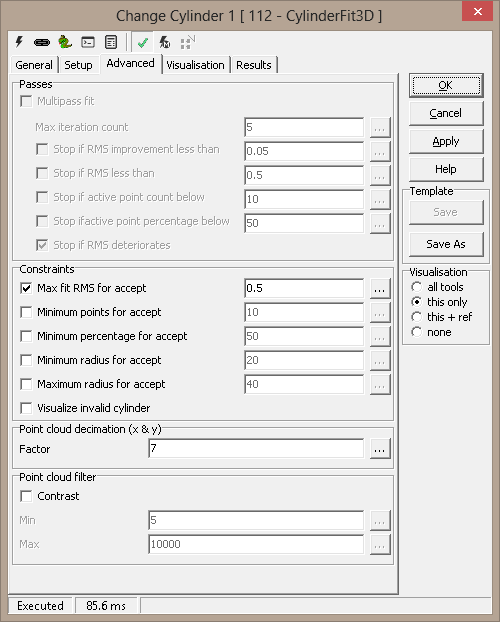
Advanced
Passes
The cylinder fit can run a multipass fit procedure. The first option is
used to turn this on or off. (This is not available for the
Exhaustive search.)
- Multipass fit - selects single or multiple passes
- Max iteration count - never exceed this number of passes
- Stop if RMS improvement less than - do not process further if
RMS does not improve more than the threshold
- Stop if RMS less than - do not process further if RMS has
reached the threshold
- Stop if active point count below - do not process further if
less than the specified number of points remain
- Stop if active point percentage below - do not process
further if less than the specified percentage of points within the ROI
remain
- Stop if RMS deteriorates - do not process further, and ignore
last pass, if RMS increases
Constraints
- Point accept distance - used to filter outliers in multipass
fit and for the result (this is not used by the Exhaustive
search)
- Max fit RMS for accept - RMS filter to accept/decline the
result
- Minimum points for accept - point count filter to
accept/decline the result
- Minimum percentage for accept - point percentage filter
(within ROI) to accept/decline the result
Point cloud decimation (x & y)
- Factor - keep only every nth sample in x and y
directions
Point cloud filter
- Contrast - element 4 in a 5-element point cloud; set min and
max allowable value
Visualisation
|
Cylinder |
Found cylinder |
|
FittedPoints |
Accepted points within the ROI |
|
InitialGuess |
Initial cylinder guess |
|
Points |
All points within the ROI |
|
ROI |
The ROI cube/cylinder segment |
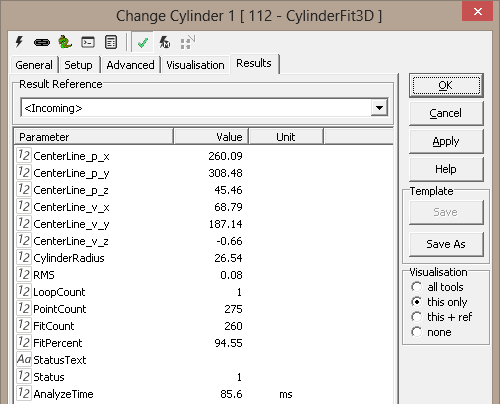
Results
|
CenterLine.p.x |
Point p and extent v form the axis within the found |
|
CenterLine.p.y |
cylinder segment. |
|
CenterLine.p.z |
|
|
CenterLine.v.x |
|
|
CenterLine.v.y |
|
|
CenterLine.v.z |
|
|
Cylinder radius |
Radius of found cylinder |
|
RMS |
Quality of fit |
|
Loop count |
Total number of loops |
|
Point count |
Total number of points within ROI |
|
Fit count |
Used points |
|
Fit percent |
Percentage of points used |
|